
Wetterthema Klima und Extreme
Durch die Klimaerwärmung wird es im Mittel wärmer, aber noch stärker verändern sich Extreme.
Erinnern Sie sich noch an die Zehn-Mark-Scheine? Auf ihnen war Carl Friedrich Gauß (1777 bis 1855) abgebildet, einer der größten Mathematiker aller Zeiten. Auf der Rückseite war die von ihm eingeführte Gaußsche Glockenkurve zu sehen. Diese findet neben der Ausschmückung von Geldnoten ebenfalls in vielen Bereichen von Naturwissenschaft und Technik Anwendung, auch in der Klimatologie. Denn sie kann uns erklären, wieso Extreme bei einer scheinbar mäßigen Erwärmung deutlich öfter auftreten sollten.
Man nehme ein Holzbrett und bestücke es in gleichmäßigen Abständen mit Nägeln, ähnlich einem Fakir-Sitzkissen. Nun verschließt man das Ganze mit einer durchsichtigen Abdeckung und stellt es senkrecht auf. Darunter stellt man mehrere kleine Behälter dicht nebeneinander und von oben lässt man dann mittig kleine Kugeln durch den Nagelwald fallen.
Die Kugeln werden von den Nägeln zufällig nach links oder rechts abgelenkt. Unten angekommen plumpsen sie in einen der Auffangbehälter. Die meisten der Kugeln werden wohl in den mittleren Behältern landen, manche jedoch fallen weiter nach außen und ganz selten kann es auch vorkommen, dass eine immer nur in eine Richtung abgelenkt wird und am Ende in eines der ganz außen stehenden Töpfe fällt.
Die sich so ergebende Verteilung in den Töpfen wir durch die von Gauß eingeführte Normalverteilung beschrieben. Sie kommt immer dann zur Anwendung, wenn die Abweichungen vom Mittelwert, also dem mittleren Topf, rein zufällig sind, größere Abweichungen jedoch zunehmend unwahrscheinlicher werden. Betrachtet man die durchschnittliche Temperatur in Deutschland über mehrere Jahre, so findet man auch hier die Normalverteilung wieder. Kühle und wärmere Jahre scheinen sich also zufällig abzuwechseln.
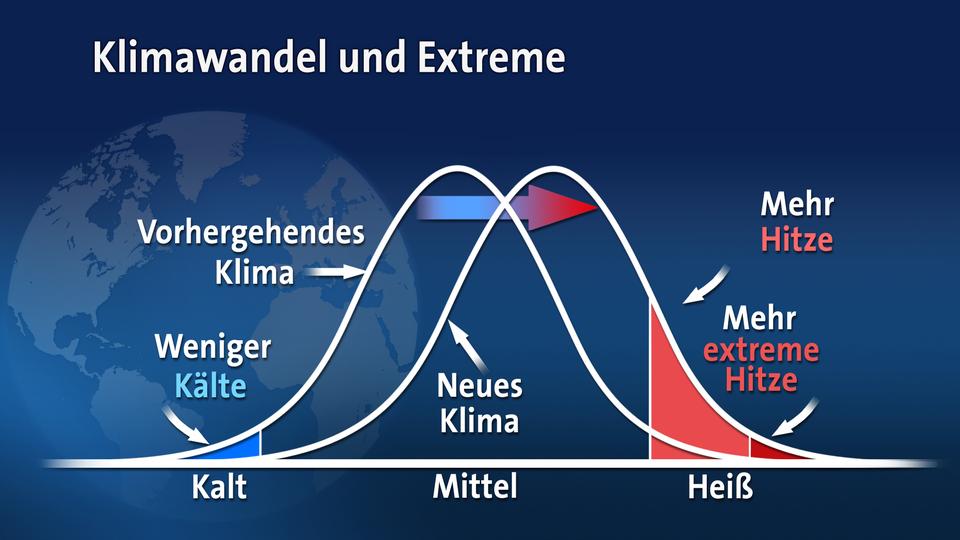
Statistische Verteilung beschreibt die Wahrscheinlichkeit für das Auftreten von Extremen
Seit ein paar Jahrzehnten verzeichnet man jedoch eine systematische Erwärmung, welche einer Verschiebung der Abwurfstelle in unserem Nagelbrett-Experiment entspricht. Die Verteilung der Kugeln in den Töpfen wird sich dadurch systematisch in eine Richtung verschieben. Interessant ist nun die Frage, wie stark sich die Anzahl der Kugeln in den äußeren Töpfen ändert. Auf das Klima übertragen entspricht das beispielsweise besonders heißen Sommern oder eben auch milden Wintern.
Die Wahrscheinlichkeit für diese Ereignisse entspricht der Fläche unter der Glockenkurve jenseits einer gewählten Temperaturschwelle. Im Nagelbrett-Experiment ist dies die Anzahl der Kugeln in den äußeren Töpfen im Vergleich zur Gesamtzahl. Aufgrund der speziellen Form der Glockenkurve verändert sich die Menge der Kugeln außen sehr stark, wenn man die Abwurfstelle nur geringfügig verschiebt. Analog steigt beispielsweise die Wahrscheinlichkeit für Hitzesommer oder auch für milde Winter hierzulande bei einer scheinbar geringfügigen Temperaturerhöhung deutlich an.
Zum Beispiel betrug die Wahrscheinlichkeit, dass die mittlere Temperatur im August in Frankfurt am Main über 22 Grad liegt im Jahre 1901 nur 0,1 Prozent. Man erwartete damals also solch einen heißen August nur etwa einmal pro Jahrtausend. Bis heute ist die Wahrscheinlichkeit auf über 15 Prozent angestiegen, somit wird aktuell etwa jeder sechste August so warm. Eine Jahresmitteltemperatur über 11,5 Grad erwartete man im Jahre 1826 in Frankfurt ebenfalls nur einmal in ungefähr 1000 Jahren. Heute wird bereits durchschnittlich alle zwei Jahre ein höherer Wert gemessen.




